After seing the article Does the centripetal force do some work? some questions arise: why we could’n see it before? Why are there so many respectable books claiming this? I think I have a culprit: a well known figure that clearly explains why there is no work done when a force is perpendicular to displacement. Yes, it’s all about a simple image. However I must admit it is a very convincing one. Haven’t I found accidentally the asteroid problem we still stay under its hypnotic power.

Let me show, your highness, the innocent gilty of 200 years of conceptual darkness:

The “Classical” graphical demonstration of the work formula.

Is a really convincing one, don’t you think? However I must say, to its favor, that the image is clear and has ever tried to trick us. This figure is only guilty of being misunderstood.

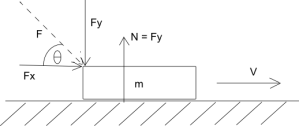
First, let’s check what the image is showing us: it is a simple block, moving over the floor, and an arrow showing us the force applied. Of.course, there is the already classical $latex \Theta$ angle, pointing out that the force is applied at an angle. The block moves only horizontally (what other direction could it take for christ sake?), so it’s obvious that only the horizontal component of the applied force will do work over the mass. That is what we always have seen. Is there any else?

The normal force acting against the vertical component.

Yes! There is a normal force, pointing upwards, equal to the vertical component of the applied force. Don’t you see it? Don’t worry, nobody draws it. Can this missing arrow change things? Of course! When this arrow appears is obvious that the vertical component of the applied force is exactly cancelled by the normal force, so the net force will be zero, and zero force do zero work. There is my friend, the source of this error.

Now think for a minute: will the mass move horizontally if no floor is there to stop it? I rest my case, Your Honor.