Is interesting the kind of ideas that arise from relativity. One of the widely accepted ones are about some kind of “relativistic stresses”. As wikipedia says:

In general, it was concluded by Dewan & Beran and Bell, that relativistic stresses arise when all parts of an object are accelerated the same way with respect to an inertial frame, and that length contraction has real physical consequences.

This assertion is correct, as far as this condition is met: ” when all parts of an object are accelerated the same way with respect to an inertial frame”

However, this is a highly unnatural situation, far from the original “spirit” of the Bell’s spaceship paradox wich initial conditions say:

“Consider two identically constructed rockets at rest in an inertial frame S. Let them face the same direction and be situated one behind the other”.

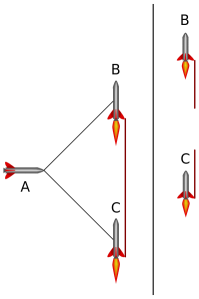
Illustration of w:Bell’s spaceship paradox with vertical motion as suggested by Bell himself, (see also File:Dewan-Beran-Bell-Paradox.svg, rocket taken from http://openclipart.org/detail/ 16043/rocket-by-mystica-16043)

It is obvious that, under this conditions, both spaceships will have exactly the same speed for every instant of time. Moreover, having the same speed they will share the same frame of reference, so B will stay at rest relative to C, and this yields to no broken thread. We can not say the same about A. A will stay at rest, so for A, B and C velocities will be different. Let’s check the facts:

Initial conditions:
$latex V_a=0\\
V_b=0\\
V_c=0\\
$

Now, let’s analyze the situation by dividing the flight time on very little intervals $latex \Delta t$, and we will assume that $latex \Delta t$ is so small that the initial condition holds for the entire interval.

Step 1 (B and C start motors). The initial conditions of this interval say $latex V_a = V_b = V_c = 0$, so A, B and C share a common reference frame, so me assume they share the reference frame for the whole $latex \Delta t$. This means $latex \Delta t_a = \Delta t_b = \Delta t_c = \Delta t$, because if A, B and C share the reference frame, time flows equally for all of them.
At the end of this step, we will have:
$latex V_a=0\\
V_b=a\Delta t\\
V_c=a\Delta t\\
V_b=V_c=V_1=a\Delta t
$

Step 2. A is a rest, while B and C has a velocity $latex V_1$. This makes B and C to share a common reference frame, while A keeps its original reference frame. This means time flows now equal to B and C, but different for A (by time dilation) $latex \Delta t_b = \Delta t_c = \Delta t$. $latex \Delta t_a \neq \Delta t$. B and C now share the same reference frame, so for all practical purposes they are at rest relative to each other. This of course means the thread doesn’t break during this interval.

$latex V_a=0\\
V_b=v_1+a\Delta t=2a\Delta t\\
V_c=v_1+a\Delta t=2a\Delta t\\
V_b=V_c=V_2=2a\Delta t
$

Step 3. A keeps at rest, while B and C has a velocity $latex V_2$. B and C share the same reference frame, so they both keep ar rest relative to each other, so no thread breaks.

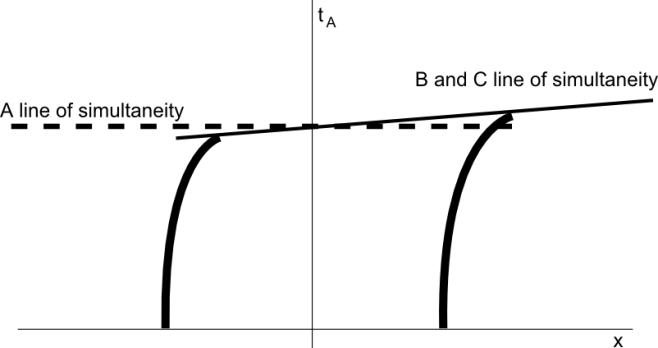
As you can see we can keep doing this analysis for a long time, and the result will not change. B and C keeps always at rest relative to each other, so the thread never breaks. Now the question is: why this was not seen before? Simple: we are humans, and by starting with A, B and C from the same reference frame and by being acceleration the same from the begining, we easily tend to think B and C will keep synchronized to A. By the way, A keeps synchronized to B and C? No. Why? By the relativity of simultaneity. When B and C get a velocity V the line of simultaneity for them get a little inclination relative to A rest frame, so simultaneous events for B and C are now out of phase for A. The phase difference is given by: $latex \Delta t=Vx/c^2$, been $latex x$ the distance from A to B or C, and V the velocity of B or C. This means (folowing our analysis) that B and C get velocity $latex V_2$ at the end of step 2 simultaneously for its own frame of reference, but B get that velocity slightly after C from the A frame of reference. This means the minkowski diagrams for this paradox are wrong too, because they assume B and C get velocity $latex V_2$ simultaneously as seen from A frame of reference. The right diagram shows below.

Bell’s spaceship paradox Minkowski diagram showing the right lines of simultaneity.

Do you see of any error in this article? Let me know! I’ll really appreciate it.