Would you like to show to your physics teacher something he doesn’t know about? Here I leave you the demonstration that the centripetal force, contrary to our beliefs, do work.

Before proceeding, let’s remember that although a circle looks like a “natural” trajectory (after all we see lots of things moving on circles), it happen that bodies don’t move ‘spontaneously’ on circular paths, but on rectilinear paths. Making a circle requires a force that changes the mass trajectory. Even more, it requires a continuous application of this force to keep it circular. Once this force disappears, the object stops making circles and start again a rectilinear motion.

What do we need to create a circle? From the cinematic point of view, all we need is a centripetal acceleration. From the dynamics point of view, all we need is a centripetal force. Now the question is: From the energy point of view, does it requires energy to make a circle? Does this centripetal force do any work over the mass moving on a circle? Or is this just a static force, making no displacement, so the total work will be zero?

Let’s see what formulas say about this.

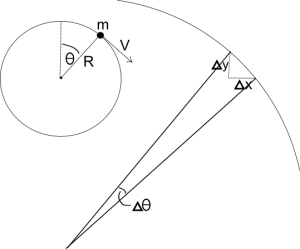
To analyze the possibility of any work done over the mass we are going to decompose the centripetal acceleration on its $latex x-y$ components, and calculate a $latex \Delta x$ and $latex \Delta y$ displacements over a $latex \Delta \Theta$ angle.

Work done by the centripetal force.

The horizontal and vertical little displacements are:
$latex \Delta x = R\Delta\Theta Cos \Theta$     (1)
$latex \Delta y = -R\Delta\Theta Sin \Theta$     (2)
Please note the minus sign, on the y direction, showing $latex \Delta y$ is decreasing ($latex y_2